ANGKA ROMAWI

Angka Dasar     
I  = 1     V = 5    X = 10   L =  50   C  = 100   D = 500  M = 1000

I     = 1                XX           = 20                   CL             = 150
II    = 2                XXXX     = 40                   CCC          = 300
III   = 3                XXXXI   = 41                    CCCL       = 350
IV   = 4                XLIV      = 44                    DXC         = 590
V    = 5                XLV        = 45                    DC            = 600
VI   = 6                L             = 50                    DCCL       = 750
VII  = 7                LXIX      = 69                    CM           = 900
VIII = 8                XC          = 90                   MX            = 1010
IX    = 9                XCI        = 91                   MCMXLV = 1945
X     = 10              C            = 100                  MMXII      = 2012

PECAHAN

A. Pengertian Pecahan

    

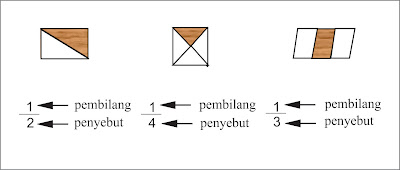
Perhatikan gambar di bawah ini.

Amati bagian gambar yang diarsir serta nilai pecahnnya.

Dari gambar tersebut, dapat dipahami bahwa pecahan terjadi karena satu benda dibagi menjadi beberapa bagian sama besar. Bagian-bagian itu mempunyai nilai pecahan.

Jadi dapat dikatakan bahwa

“Pecahan adalah beberapa bagian dari keseluruhan”

Latihan 1

Tulislah nilai pecahan untuk gambar yang berwarna kuning!

B.   Perbandingan dan Urutan Pecahan

1.     Menuliskan letak pecahan pada garis bilangan

Untuk menunjukkan letak suatu pecahan, mari kita gambarkan garis bilangan antara bilangan 0 dan bilangan 1. 

a. Dimanakah letak pecahan 1/2 ? 
b. Dimanakah letak pecahan 1/4, 2/4, 3/4 ?
Mari kita selesaikan bersama-sama.

a.      Untuk menentukan letak pecahan 1/2 , kita bagi ruas garis bilangan antara 0 dan 1 menjadi dua bagian, sehingga diperoleh garis bilangan perduaan. 

 

 

Jadi, pecahan 1/2 terletak di tengah bilangan 0 dan 1. 

b.     Untuk menentukan letak pecahan 1/4, 2/4, 3/4, kita bagi ruas garis bilangan antara 0 dan 1 menjadi empat bagian, sehingga diperoleh garis bilangan perempatan. Letak masing-masing pecahan 1/4, 2/4, 3/4 adalah sebagai berikut. 

 

Catatan:

      Bilangan dapat dituliskan dalam bentuk pecahan dengan pembilang dan penyebut yang sama 1 = 1/1 = 2/2 = 3/3 = 4/4 = ….

 

GEOMETRI

1. Bangun Ruang

1. Mengenal bangun ruang

Perhatikan benda-benda di bawah ini!

Semua benda tersebut disebut bangun ruang. Mengapa disebut bangun ruang, karena semua benda tersebut termasuk benda tiga dimensi, yang memiliki panjang, lebar. dan tinggi. Contoh-contoh bangun ruang adalah balok, kubus, kerucut, prisma, tabung, bola, dan limas. Nah sekarang coba perhatikan gambar berikut ini!

Pada gambar tersebut, adakah benda-benda yang berbentuk balok, kubus, kerucut, prisma, tabung, bola, dan, limas.

Adakah benda-benda di sekitarmu yang berbentuk seperti bangun-bangun ruang tersebut? Coba kamu sebutkan! Bagaimana sifat-sifat kubus, balok, bola, tabung, limas, prisma, dan kerucut? Mari kita pelajari bersama.

2. Macam-macam bangun datar

Dalam bangun ruang dikenal istilah sisi, rusuk, dan titik sudut. Mari kita perhatikan bangun ruang berikut ini. 

 

Sisi adalah bidang atau permukaan yang membatasi bangun ruang. Rusuk adalah garis yang merupakan pertemuan dari dua sisi bangun ruang. Titik sudut adalah titik pertemuan dari tiga buah rusuk pada bangun ruang.

Mari kita selidiki satu persatu sifat-sifat bangun ruang sederhana tersebut berkaitan dengan sisi, rusuk, dan titik sudutnya.

1. Sifat-sifat kubus

Untuk mengetahui sifat-sifat bangun ruang kubus, mari kita perhatikan gambar di bawah ini. 

 

Mari menyebutkan sisi, rusuk, dan titik sudut pada kubus ABCD.EFGH.

1. Sisi-sisi pada kubus ABCD.EFGH adalah:

• sisi ABCD - sisi EFGH
• sisi ABFE - sisi DCGH
• sisi ADHE - sisi BCGF

Jadi, ada 6 sisi pada bangun ruang kubus.

Sisi kubus tersebut berbentuk persegi (bujur sangkar) yang berukuran sama.

2. Rusuk-rusuk pada kubus ABCD.EFGH adalah:

• rusuk AB - rusuk BC - rusuk AE
• rusuk EF - rusuk FG - rusuk BF
• rusuk HG - rusuk EH - rusuk CG
• rusuk DC - rusuk AD - rusuk DH

Jadi, ada 12 rusuk pada bangun ruang kubus.

Rusuk-rusuk kubus tersebut mempunyai panjang yang sama.

3. Titik-titik sudut pada kubus ABCD.EFGH adalah:

• titik sudut A - titik sudut E
• titik sudut B - titik sudut F
• titik sudut C - titik sudut G
• titik sudut D - titik sudut H

Jadi, ada 8 titik sudut pada bangun ruang kubus.

Dari uraian diatas, dapat kita tuliskan pengertian bangun ruang kubus sebagai berikut.

“Kubus adalah sebuah benda ruang yang dibatasi oleh enam buah persegi yang berukuran sama”.

2. Sifat-sifat balok

Untuk mengetahui sifat-sifat bangun ruang balok, mari kita perhatikan gambar di bawah ini.

Mari menyebutkan sisi, rusuk, dan titik sudut pada balok ABCD.EFGH.

1. Sisi-sisi pada balok ABCD.EFGH adalah:

• sisi ABCD - sisi EFGH
• sisi ABFE - sisi DCGH
• sisi ADHE - sisi BCGF

Jadi, ada 6 sisi pada bangun ruang balok.

Sisi ABCD = sisi EFGH

Sisi BCGF = sisi ADHE

Sisi ABFE = sisi EFGH

2. Rusuk-rusuk pada balok ABCD.EFGH adalah:

• rusuk AB - rusuk BC - rusuk AE
• rusuk EF - rusuk FG - rusuk BF
• rusuk HG - rusuk EH - rusuk CG
• rusuk DC - rusuk AD - rusuk DH

Jadi, ada 12 rusuk pada bangun ruang balok.

Rusuk AB = rusuk EF = rusuk HG = rusuk DC

Rusuk BC = rusuk FG = rusuk EH = rusuk AD

Rusuk AE = rusuk BF = rusuk CG = rusuk DH

3. Titik-titik sudut pada balok ABCD.EFGH adalah:

• titik sudut A - titik sudut E
• titik sudut B - titik sudut F
• titik sudut C - titik sudut G
• titik sudut D - titik sudut H

Jadi, ada 8 titik sudut pada bangun ruang balok.

Dari uraian diatas, dapat kita tuliskan pengertian bangun ruang balok sebagai berikut.

“Balok adalah sebuah benda ruang yang dibatasi oleh tiga pasang (enam buah) persegi panjang dimana setiap pasang persegi panjang saling sejajar (berhadapan) dan berukuran sama”.

3. Sifat-sifat tabung, kerucut, dan bola

Tabung, kerucut, dan bola sangat berbeda dengan kubus maupun balok. Dalam ketiga bangun ruang ini terdapat sisi yang melengkung. Untuk mengetahui sifat-sifat bangun ruang tabung, mari kita perhatikan gambar di bawah ini. 

Bangun ruang tabung mempunyai 3 buah sisi, yaitu sisi lengkung, sisi atas, dan sisi bawah. Tabung mempunyai 2 buah rusuk, tetapi tidak mempunyai titi sudut.

Bangun ruang kerucut mempunyai dua buah sisi, yaitu sisi alas dan sisi lengkung. Kerucut hanya mempunyai sebuah rusuk dan sebuah titik sudut yang biasa disebut titik puncuk.

Yang terakhir, bangun ruang bola hanya memiliki sebuah sisi lengkung yang menutupi seluruh bagian ruangnya.

Latihan 1

Lengkapilah tabel berikut ini!

Bangun ruang	Banyak sisi	Banyak rusuk	Banyak titik sudut

2. Jaring-jaring bangun ruang

1. Jaring-jaring kubus dan balok

Bangun ruang kubus dan balok terbentuk dari bangun datar persegi dan persegi panjang. Gabungan dari beberapa persegi yang membentuk kubus disebut jarring-jaring kubus. Sedangkan jaring-jaring balok adalah gabungan dari beberapa persegi panjang yang membentuk balok. Bagaimana bentuk jaring-jaring kubus? Coba perhatikan gambar dibawah ini. 

 

                                                              Jaring-jaring kubus 

                                                             jaring-jaring balok

Itu adalah contoh gambar jaring-jaring kubus dan balok. Nah sekarang, adakah bentuk jaring-jaring kubus yang lain? Coba kalian selidiki dan diskusikan dengan teman-temanmu.

2. Jaring-jaring tabung dan kerucut

Bangun ruang tabung dan kerucut terbentuk dari alas lingkaran. Jaring-jaring tabung terdiri dari 3 bangun datar, yaitu 2 lingkaran dan 1 persegi panjang (selimut). Bagaimana bentuk jaring-jaring tabung dan kerucut? Coba perhatikan gambar di bawah ini. 

                                                                    Jaring-jaring tabung 

                                                                    jaring-jaring kerucut

Latihan 2

Coba lingkari manakah di antara gambar berikut yang merupakan jaring-jaring kubus!

BILANGAN ROMAWI

A.   Mengenal Lambang Bilangan Romawi

      HUT Republik Indonesia LXVI, yaitu HUT RI yang ke-66 diperingati dengan meriah di seluruh pelosok tanah air.

      LXVI adalah lambang bilangan Romawi untuk bilangan 66. Bilangan Romawi tidak banyak digunakan dalam kehidupan sehari-hari Mari kita perhatikan contoh-contoh kalimat berikut:

1.     Yani tinggal bersama kakeknya di Jalan Anggrek XII nomor 20

2.     Memasuki abad XXII, kita dituntut untuk lebih menguasai IPTEK dan IMTAQ

Coba kamu perhatikan kembali huruf-huruf yang dicetak tebal pada contoh-contoh kalimat diatas. XII, XXII merupakan bilangan-bilangan romawi. Coba kamu sebutkan contoh penggunaan bilangan romawi lainnya yang kamu ketahui.

Bagaimana lambang bilangan romawi? Secara umum, bilangan romawi terdiri dari 7 angka (dilambangkan dengan huruf) sebagai berikut. 

I    Melambangkan bilangan 1 

V  Melambangkan bilangan 5 

X  Melambangkan bilangan 10 

L  Melambangkan bilangan 50

C  Melambangkan bilangan 100 

D  Melambangkan bilangan 500 

M Melambangkan bilangan 1000

  

     Untuk bilangan-bilangan  yang lain, dilambangkan oleh perpaduan (campuran) dari ketujuh lambang bilangan tersebut.

B.    Membaca Bilangan Romawi

Pada sistem bilangan romawi tidak dikenal bilangan 0 (nol). Untuk membaca bilangan romawi, kamu harus hafal dengan benar ketujuh lambang bilangan dasar Romawi.

Bagaimana aturan-aturan dalam membaca lambang bilangan romawi? Bagaimana menyatakan bilangan Romawi ke bilangan asli? Mari kita pelajari bersama.

1.     Aturan penjumlahan bilangan romawi

Untuk membaca bilangan romawi, dapat kita uraikan dalam bentuk penjumlahan seperti pada contoh berikut ini.

Contoh:

a.      II           = I + I

                   = 1 + 1

                   = 2

b.     LXXVI  = L + X + X + V + I

                   = 50 + 10 + 10 + 5 + 1

                   = 76

Coba kamu perhatikan lambang bilangan romawi pada contoh-contoh diatas. Semakin ke kanan, nilainya semakin kecil. Tidak ada lambang bilangan dasar yang berjajar lebih dari tiga.

Dari contoh-contoh tersebut dapat kita tuliskan aturan pertama dalam membaca lambang bilangan romawi sebagai berikut.

a.      Jika lambang yang menyatakan angka lebih kecil terletak di kanan, maka lambang-lambang romawi tersebut dijumlahkan.

b.     Penambahnya paling banyak tiga angka. 

2.     Aturan pengurangan bilangan romawi

Untuk membaca bilangan romawi, dapat kita uraikan dalam bentuk pengurangan seperti pada contoh berikut ini.

 Contoh:

a.      IX         = X – I

                   = 10 – 1

                   = 9

      Jadi, IX dibaca 9

b.     XL        = L – X

                   = 50 – 10

                   = 40

      Jadi, XL dibaca 40 

Dari contoh-contoh tersebut dapat kita tuliskan aturan kedua dalam membaca lambang bilangan romawi sebagai berikut.

a.      Jika lambang yang menyatakan angka lebih kecil terletak di kiri, maka lambang-lambang romawi tersebut dikurangkan.

b.     Pengurangannya paling banyak satu angka.

3.     Aturan gabungan

Dari kedua aturan di atas (penjumlahan dan pengurangan) dapat digabung sehingga bisa lebih jelas dalam membaca lambang bilangan romawi.

Mari kita perhatikan contoh berikut ini.

Contoh:

a.       XXIX = X + X + (X – I)

            = 10 + 10 + (10 -1)

            = 20 + 9

            = 29

Jadi XXIX dibaca 29

b.      MMIX    = M + M + (X – I)

                = 1000 + 1000 + (10 - 1)

                = 2000 + 9

                = 2009

Jadi, MMIX dibaca 2009

C.    Menulis lambang bilangan romawi

Dalam menulis lambang bilangan romawi, perlu diperhatikan ketentuan berikut:

1.     Lambang yang sama hanya boleh berurutan 3 kali.

Contoh:          3       = III

                      30     = XXX

                      4 tidak boleh ditulis IIII

2.     Bila lambang yang nilainya lebih kecil terletak di sebelah kanan lambang yang nilainya lebih besar, berarti penjumlahan.

Contoh:         VII   = 5 + 2 = 7

                      XI    = 10 + 1 = 11

Sebaliknya, bila lambang yang nilainya lebih kecil terletak di sebelah kiri lambang yang nilainya lebih besar berarti pengurangan.

Contoh:         IV    = 5 – 1 = 4

                      XL   = 50 – 10 = 40

3.     V dan X hanya dapat dikurangi oleh I, sedangkan L hanya dapat dikurangi oleh X, itu pun terbatas satu lambang.

Contoh:         9       = IX

                      3 tidak boleh ditulis IIV

                      30 tidak boleh ditulis XXL

D.   Mengubah lambang bilangan asli ke lambang bilangan romawi

Contoh:

45       = XLV                    LIX     = 59

32       = XXXII                XXVI   = 26

E.    Pemakaian lambang bilangan romawi

Lambang bilangan romawi sering dipakai untuk:

1.     Menulis tingkatan kelas

Contoh: Kelas I, Kelas II, Kelas III, Kelas IV, Kelas V, Kelas VI

2.     Menulis nomor sekolah dasar

Contoh: SDN Bintang XI

              SD Cakra Mawar V

3.    Menulis bilangan pada jam

4.    Menulis nomor bab dalam buku

Contoh: Bab I      Pendahuluan

              Bab II     Belajar Bekerjasama

              Bab III   Belajar kelompok   

Latihan

1.     Ubahlah menjadi lambang bilangan romawi!

a.      15

b.     33

c.      91

d.     280

e.      2016

2.     Ubahlah menjadi bilangan cacah!

a.      XLVII

b.     LXXVIII

c.      CCCXXXVIII

d.     CDXLIV

e.      MDCXVI